【経済学・経済政策】無差別曲線マスター講座｜基本理論から特殊な形状まで徹底解説

中小企業診断士の一次試験科目である経済学・経済政策では、「無差別曲線」を用いて消費者の行動を分析します。

「無差別曲線」は、ミクロ経済学の中でも基本となる内容であり、中小企業診断士試験でも頻出の分野となっているため、経済学・経済政策を攻略する上で必ず理解しておくべきです。

しかし、無差別曲線では経済学特有の考え方・グラフを使って理論を説明するため、特に経済学の初学者であれば理解するのに時間を要することも事実です。

この記事では、「無差別曲線」の基本的な考え方から、特殊な形状の無差別曲線まで、中小企業診断士試験で出題される論点に絞って解説します。

無差別曲線に関する問題は、考え方さえ理解できれば確実に得点できるため、経済学・経済政策で安定した点を取るための武器とできる分野でもあります。

この記事を読めば、経済学・経済政策において、無差別曲線に関する応用的な問題まで対応し、得点源にできるようになるはずです。

効用関数

無差別曲線を理解するためには、「効用」について知っておく必要があります。

まずはじめに、前提知識となる「効用」について整理しておきましょう。

「効用」と「選好」とは

消費者は、財を消費することで満足度を得ています。

このとき、ある財を消費することで得られる満足度のことを「効用」と呼びます。

効用：ある財を消費することから得られる満足度のこと

また、ある財を消費することによって得られる満足度は人によって様々です。

例えば、アイドルのファンがグッズを購入する満足感は高いですが、そのアイドルに興味がない人がグッズを買っても満足感はないですよね。

このような、人々の好みの違いを「選好」と呼びます。

選好：人々によって異なる好みのこと

効用関数とは

次に、「効用」を数値化・関数化することで、消費者の行動を分析できるようにします。

このときに用いられるのが「効用関数」です。

効用関数：効用を数値化して関数化したもの

定義を聞いてもイマイチ理解しにくいですので、グラフを使って解説します。

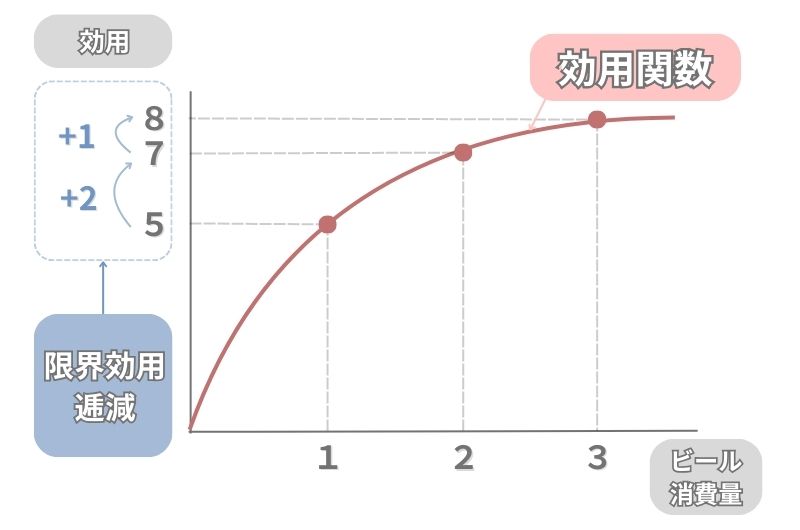
このグラフでは、横軸には「ビールの消費量」を、縦軸には「ビールを消費したときに得られる効用」を置きます。

このとき、ビールの消費量が増えると効用が大きくなっていることが分かります。

ビールに限らず、モノを消費するときは多く消費できるほどうれしいですよね。

しかし、このグラフの効用関数は右上がりの曲線になっています。

これは、ビールを飲む量が増えると一杯当たりの価値が低くなり、得られる効用が小さくなっていくことを意味しています。

この時、ビールの消費量を一杯増やしたときに増加する効用のことを「限界効用」と呼びます。

限界効用：財の消費量を一単位増加させたときに得られる効用の大きさ

そして、ビールの消費量が増えるほど一杯当たりの価値が薄くなり、得られる効用が小さくなることを「限界効用が逓減している」と言います。

限界効用の逓減：財の消費量が増えるほど限界効用が小さくなっていくこと

ビールは最初の一口が一番おいしいですよね。たくさん飲んでいるとレモンサワーが飲みたくなってくるのは、ビールに対する限界効用が逓減しているからです！

ここまでが、無差別曲線を理解する上での前提知識となる「効用関数」についての解説です。

無差別曲線

ここからは、無差別曲線について解説します。

「無差別曲線」とは

ここまで効用関数について解説してきましたが、あくまで１つの財を消費するパターンを考えてきました。

一方で、無差別曲線では、２つの財を消費する組み合わせを考えていきます。

そして、その人にとって同じ満足度を得られる２つの財の消費量の組み合わせを結んだ曲線を「無差別曲線」と呼びます。

無差別曲線：２つの財を消費するときに、同じ効用が得られる消費量の組み合わせを示した曲線

こちらも言葉ではイメージしにくいので、グラフを使って解説していきます。

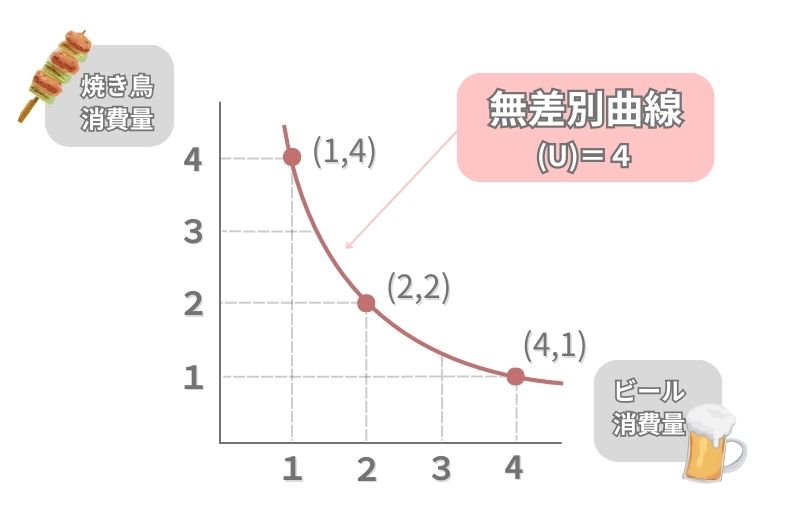
このグラフでは、横軸に「ビールの消費量」を、縦軸に「焼き鳥の消費量」を取ります。

無差別曲線では、ビールと焼き鳥を消費するときに、同じ満足感が得られる組み合わせを結んでいきます。

このグラフにおいては、U（効用）＝ビールの消費量(x)×焼き鳥の消費量(y)が「４」になる消費量の組み合わせを結んだ無差別曲線を図示しています。

無差別曲線の「４つの性質」

基本的な無差別曲線が持つ、「４つの性質」について解説します。

この性質を持たない無差別曲線については、例外として後ほど解説します。

右下がりの曲線になる

基本的な無差別曲線は、必ず右下がりの曲線になります。

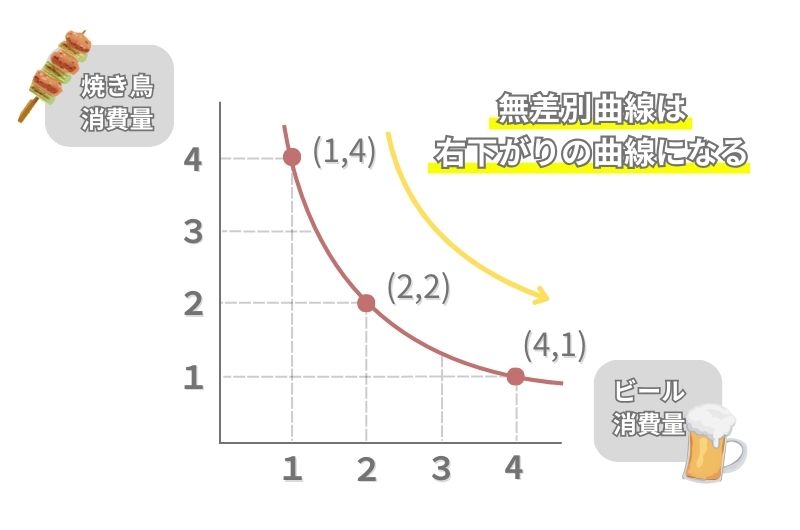
右下がりの曲線になるとは、「ビールの消費量が増えたら焼き鳥の消費量は減る」ことを意味しています。

ビールの消費量が増え、焼き鳥の消費量も増えてしまったら、トータルの効用水準が高くなってしまい、同じ無差別曲線上に存在しなくなってしまいます。

これを言い換えると、ビールの消費量が一定であれば、焼き鳥の消費量が増えたら必ず効用水準が高くなることになり、この性質を「単調性」と呼びます。

単調性：一方の財の消費量が一定のとき、他方の財の消費量が増えた場合には、必ず効用水準が高くなる

このように、無差別曲線は、同じ効用水準を結んだ曲線であるため、一方の財の消費量が増えたときは、他方の財の消費量は減ることになるため、右下がりの曲線になるはずなのです。

右上にある無差別曲線に方が効用水準が高い

単調性が成り立っている場合には、右上にある無差別曲線の方が効用水準が高いという性質があります。

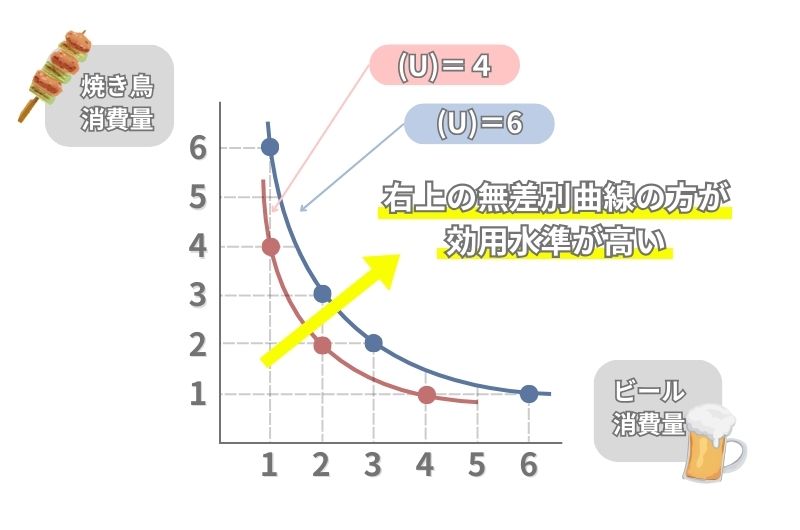
このグラフを見ると、赤色の無差別曲線は効用水準が「４」、青色の無差別曲線は効用水準が「６」になっています。

ビールを１消費しているとき、赤色の無差別曲線では焼き鳥を４、青色の無差別曲線では６消費できていますね。

これは、より多くの財を消費できている右上の無差別曲線の方が効用水準が高いことを意味しています。

交わることがない

３つ目の特徴は、無差別曲線は必ず交わらないことです。

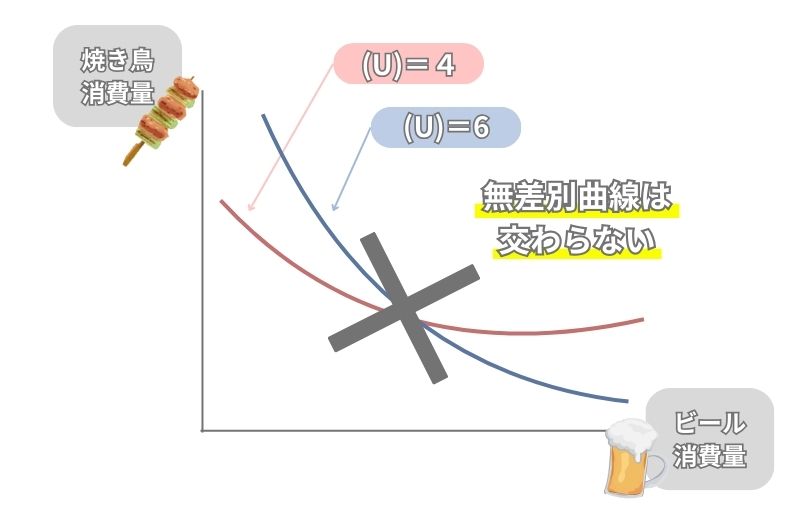
無差別曲線は、同じ効用水準が得られる組み合わせを結んだ曲線であることをお話ししました。

もし、効用水準「４」の無差別曲線と効用水準「６」の無差別曲線が交わってしまったら、その交点では効用水準が「４」か「６」のどちらかとわからないですよね。

このように、2つ以上の無差別曲線が交わってしまえば、効用水準に矛盾が生じるため、無差別曲線が交わることはありません。

原点に対して凸の曲線になる

基本的な無差別曲線は、必ず原点に対して凸な形状をした曲線になることも特徴です。

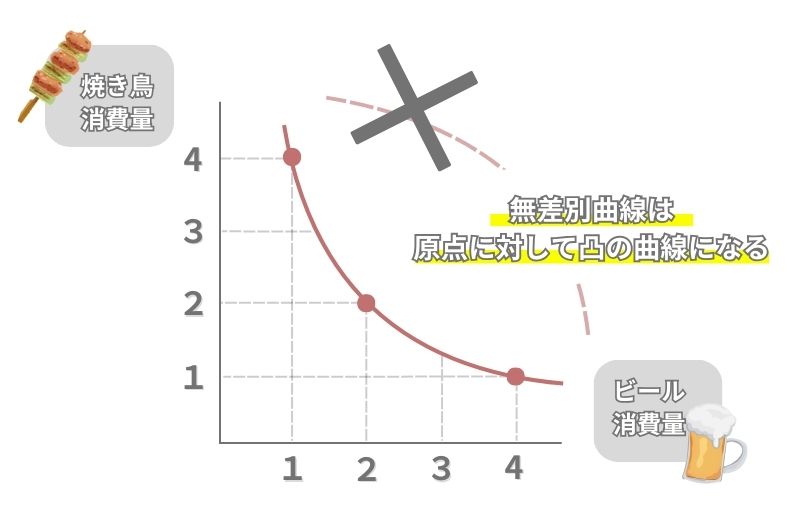
「原点に対して凸な曲線」とは、原点から見て内側に曲がっている形状のことです。

無差別曲線が原点に対して凸な形状になるのは、「限界代替率」という考え方によって説明できます。

結論を先に述べると、「限界代替率が逓減する」ため、無差別曲線は原点に凸の形状になります。

「限界代替率」については、下で解説します。

限界代替率

上記で、無差別曲線は、限界代替率が逓減するため、原点に対して凸の曲線となるとお話ししました。

ここでは、その「限界代替率」とは何かについて解説します。

「限界代替率」とは

ここまで見てきた無差別曲線は、2つの財を消費するとき、同じ満足感が得られる組み合わせを結んだ曲線です。

同じ満足感を得るということは、仮にどちらかの財の消費量が増えたら、もう一方の財の消費量は減らなければおかしいですよね。これは、無差別曲線が右下がりになることの理由とお話ししました。

このとき、一方の財の消費量が変化したとき、同じ満足度を維持するために必要な、もう一方の財の変化量のことを「限界代替率」と呼びます。

限界代替率：一方の財の消費量が変化したとき、同じ効用水準を維持するために必要な、もう一方の財の変化量

言葉ではわかりにくいので、こちらもグラフを用いて解説します。

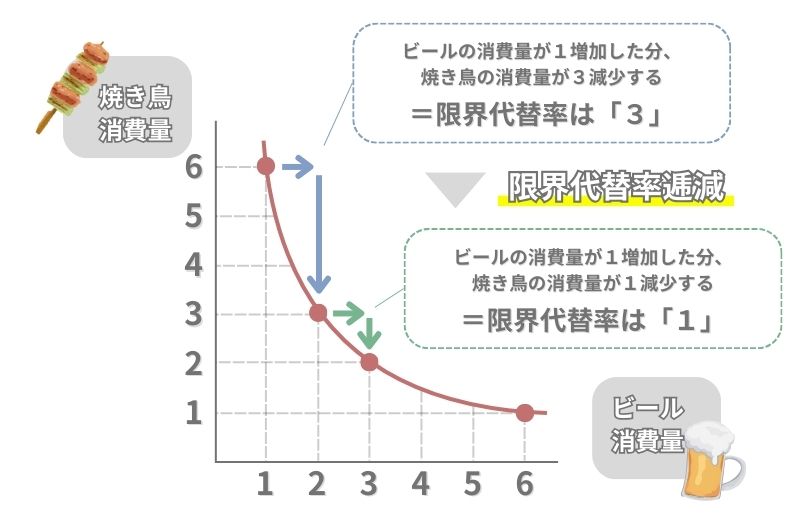
このグラフを見ると、ビールの消費量を１個から２個に増やしたとき、同じ満足度を得ることのできる焼き鳥の消費量が６個から３個に減少しています。この時の焼き鳥の変化量が限界代替率であり、限界代替率は「３」となります。

一方、ビールの消費量を２個から３個に増やしたとき、同じ満足度を得ることのできる焼き鳥の消費量が３個から２個に減少しています。つまりこの時の限界代替率は「１」となります。

おつまみ無しでビールだけ飲んでいると飽きてきますよね。２杯目のビールには焼き鳥３本分の価値を感じていたのに、３杯目には焼き鳥１本分の価値しか感じていないわけです。

このように、ビールの消費量が増加するにつれて、焼き鳥の変化量が減少して限界代替率が小さくなっていくことを、「限界代替率逓減」と呼びます。

限界代替率逓減：一方の財の変化量が増加するにつれ、効用の維持に必要なもう一方の変化量が小さくなる

限界代替率＝無差別曲線への接線への傾き

この論点については、「限界代替率＝無差別曲線への接線の傾き」と覚えてしまいましょう。

簡単に図で説明すると以下のようになります。

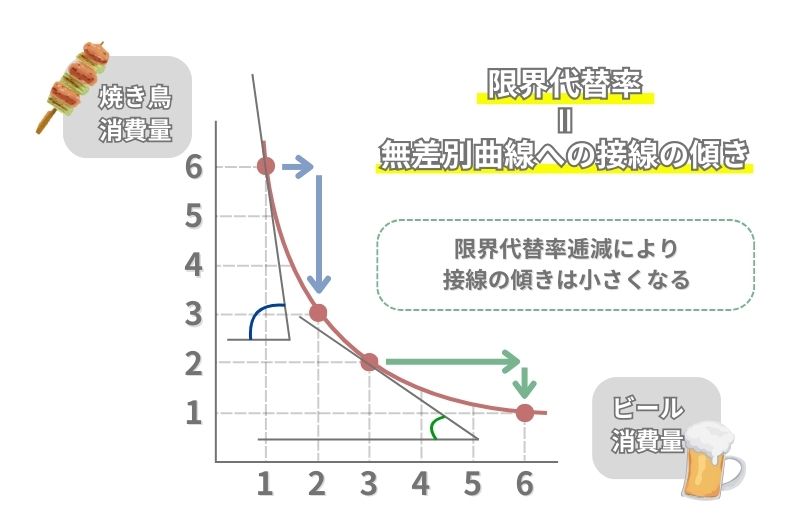
このグラフでは、ビールの消費量が１個の時と３個の時の接線の傾きを比較しています。

ビール３個目のタイミングではビールに飽きてきているため、焼き鳥の変化量はかなり小さい（ビールに価値を感じていない）状態でしょう。

つまりこのタイミングは、ビール１個の時よりも限界代替率が小さい状態であり、無差別曲線への接線の傾きが小さくなっていることが分かります。

そして、この限界代替率逓減により無差別曲線の傾きは徐々に小さくなっていくため、無差別曲線は原点に対して凸の曲線になります。

様々な形の無差別曲線

ここまでお話ししてきた無差別曲線は、２つの財を消費するときの一般的な消費動向に基づくものです。

ここでは、今までお話ししてきたものとは異なる、特殊な形状の無差別曲線について解説します。

L字型

２つの財が「完全補完財」である組み合わせの時、無差別曲線はL字型の形状になります。

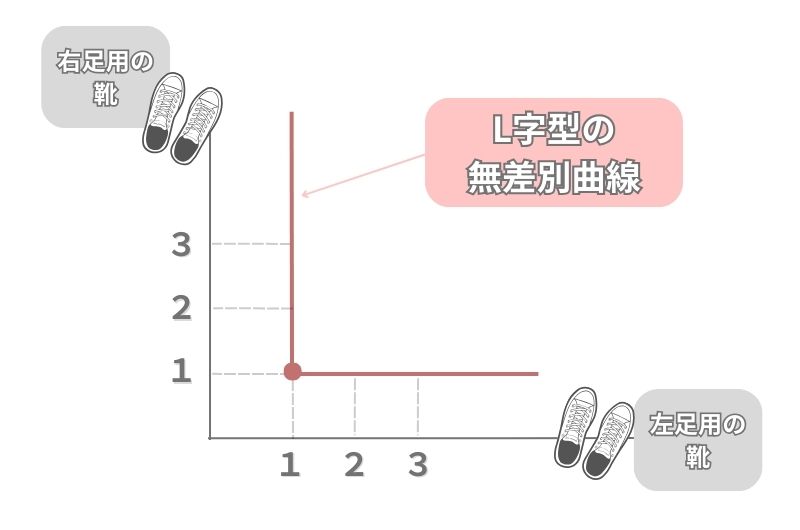
「完全補完財」とは、簡単に言えば、両財が2つ揃って初めて価値が生まれる財の組み合わせのことです。

上記のグラフでは、縦軸に「右足用の靴」を、横軸に「左足用の靴」を取っています。

靴は右足・左足用の２つが揃ってはじめて機能するものですので、右足用の靴が１個しかないときに左足用の靴だけがいくら増えても、効用水準には一切影響を与えません。

このように、完全補完財の組み合わせでは、片方だけが増えても効用水準に影響を与えないため、無差別曲線はL字型の形状になります。

L字型の無差別曲線：消費する財の組み合わせは「完全補完財」である

右下がりの直線

２つの財が「完全代替財」である組み合わせの時、無差別曲線は右下がりの直線になります。

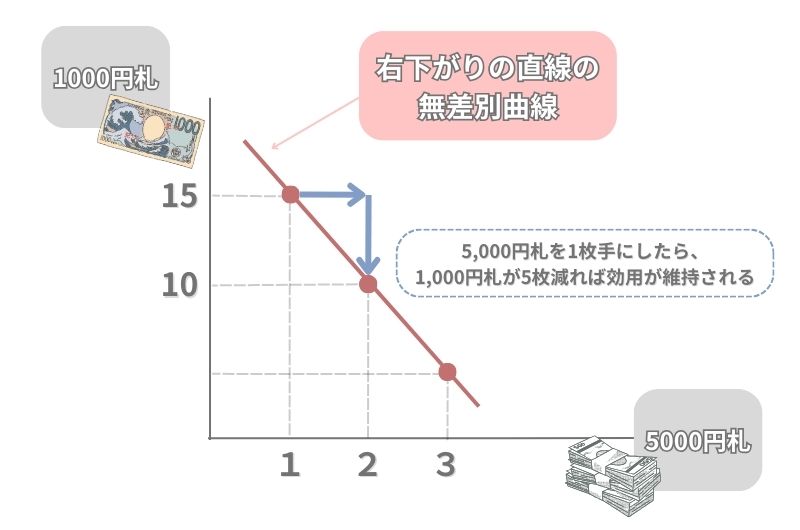
「完全代替財」とは、簡単に言えば、どちらでもいい２つの財の組み合わせのことです。

上記のグラフでは、縦軸に「1,000円札」を、横軸に「5,000円札」を取っています。

5,000円札１枚は、1,000円札５枚と同じ価値であることは絶対に代わりませんよね。同じ効用を維持するには、5,000円札が１枚増えた時には1,000円札を５枚減らせばいいわけです。

このように、完全代替財の組み合わせでは限界代替率が逓減しないため、無差別曲線は直線になります。

右下がりの直線である無差別曲線：消費する財の組み合わせは「完全代替財」である

右上がりの曲線

片方の財が、消費量が増えると効用が減少するものであると、無差別曲線は右上がりの曲線になります。

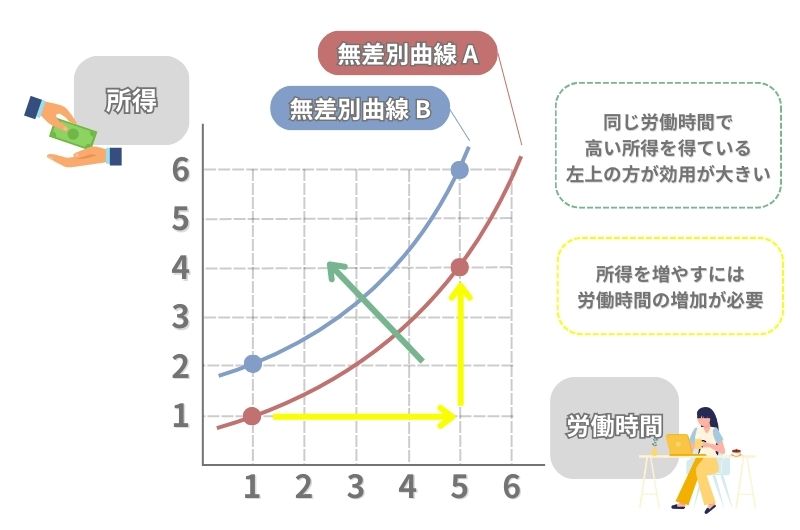
財の中には、その消費量が増えることで効用が減少してしまうものも存在します。

このグラフでは、縦軸に「所得」を、横軸に「労働時間」を取っています。

この場合、もちろん所得は増えるほど効用が高まります。しかし、一般的には労働時間の増加は嬉しいものではないので、労働時間の増加によって効用は下がりますが、所得を得るためには必要です。

つまり、労働時間が短い時は少ない所得でも納得できるが、たくさん労働したときにはその労働に見合った所得の増加が無ければ効用水準を維持できないわけです。

これゆえに、一方の財が消費量の増加により効用が減少する財であるときには、無差別曲線は右上がりの曲線になります。

また、このような右上がりの曲線である無差別曲線は、左上に位置する方が効用水準が高くなります。

これは、労働時間が「１」の時、赤色の無差別曲線では所得が「１」、青色の無差別曲線では所得が「２」であり、同じ労働時間でも得ている所得が多いことを確認するとわかりやすいです。

右上がりの曲線である無差別曲線：一方の財が、消費量の増加により効用が減少するものである

過去問と解答

中小企業診断士試験で出題された、無差別曲線に関する過去問と解説を紹介します。

令和3年度　第15問

令和3年度　第15問

下図のような形状をした無差別曲線に関する記述として、最も適切な組み合わせを下記の解答群から選べ。【引用】中小企業診断士試験問題 (j-smeca.jp)

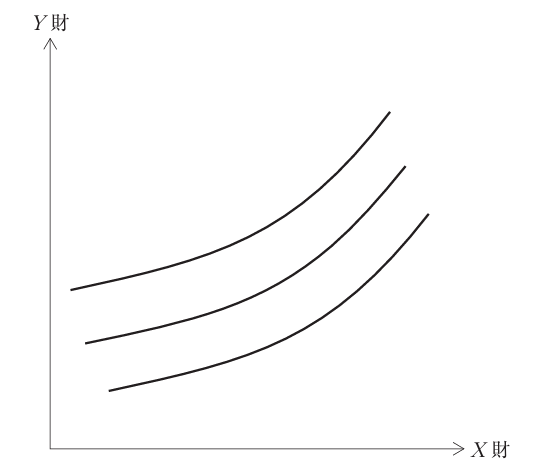
ａ　X財がおにぎり、Y財がサンドイッチのように、不完全であるが代替可能性のある2財の関係を示している。

ｂ　X財がお弁当、Y財が容器ゴミのように、通常の財と負の財の関係を示している。

ｃ　この無差別曲線上におけるX財とY財の組み合わせでは、得られる効用は一定である。

ｄ　この無差別曲線上を右に行くほど、X財を1単位増やすために減らさなければならないY財の量は増加する。

〔解答群〕
ア　ａとｃ
イ　ａとｃとｄ
ウ　ｂとｃ
エ　ｂとｃとｄ
オ　ｂとｄ

↓答えを決めてからスクロールして解答をチェック！↓

解答解説

a：適切ではない
X財がおにぎり、Y財がサンドイッチのように、不完全であるが代替可能性のある2財の関係を示している。

➤➤「不完全であるが代替可能性のある2財の関係」を示す無差別曲線は、右下がりの曲線になり、いわゆる基本的な形状のものになるはずです。また、「完全代替財である2財」であれば、右下がりの直線になります。

b：適切である
X財がお弁当、Y財が容器ゴミのように、通常の財と負の財の関係を示している。

➤➤この問題で図示されている無差別曲線は、「右上がりの曲線」です。つまり、片方の財が消費量の増加によって効用が減少するもの（負の財）であり、容器ゴミが該当します。

c：適切である
この無差別曲線上におけるX財とY財の組み合わせでは、得られる効用は一定である。

➤➤無差別曲線の基本に立ち返りましょう。無差別曲線は、「同じ効用水準が得られる2財の組み合わせを結んだ曲線」ですので、同じ無差別曲線上であれば得られる効用は一定になります。

d：適切ではない
この無差別曲線上を右に行くほど、X財を1単位増やすために減らさなければならないY財の量は増加する。

➤➤この右上がりの曲線における2財は、X財（通常の財）を増やすために、Y財（負の財）も増やさなければならないという関係を持っています。つまり、「減らさなければならない」ではなく「増やさなければならない」という文言でなければいけません。また、右に行くほど無差別曲線の傾きが急になっているため、限界代替率が逓増している点は正しいです。

よって、記述が正しい「b」と「c」の組み合わせである「ウ」が正解です。

まとめ

当記事を最後までお読みいただき、ありがとうございます。

今回は、ミクロ経済学の基本的な内容であり、中小企業診断士試験にも頻出の「無差別曲線」について、基本的な考え方から特殊な形状のものまで、試験攻略に必要な知識を解説させていただきました。

近年の無差別曲線に関する問題は、基本的な考え方はもちろん、特殊な形状が出題されたり、紛らわしい選択肢が含まれていたりと、一筋縄ではいかない問題が増えている傾向があります。

今回ご紹介した内容を理解しておけば、少し難解な内容が出題されても対応できるかと思います。

勉強の合間やスキマ時間に読んでいただき、無差別曲線が皆さんの得意分野になれば幸いでございます。

他にも、中小企業診断士試験を最短で合格するために役立つ記事を発信していますので、是非チェックしてみてください。